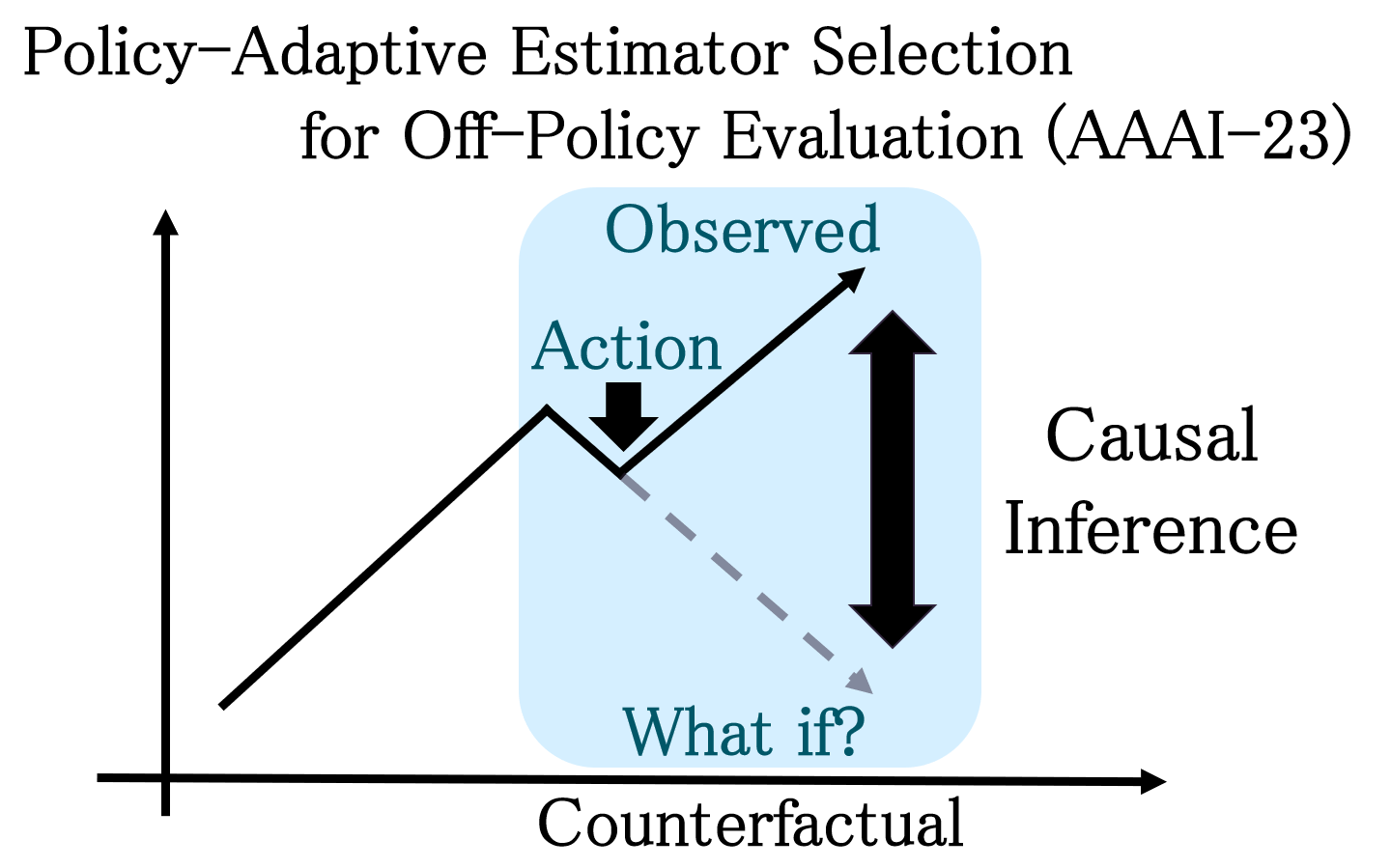
Introduction
I am Takuma Udagawa, a researcher in machine learning and causal inference at Sony Group Corporation. This article introduces some fundamentals on the offline evaluation of decision-making algorithms and the paper we presented at AAAI2023 [1].
Background
Currently, service providers take various kind of action on users in a decision-making process in many scenarios, such as recommendations in video streaming services, personalization in online advertising, and e-mail newsletters. In particular, the decision-making policy based on machine learning models trained on logged data collected in the past plays an important role in improving key performance indicator (KPI).
The optimization of the decision-making policy is also necessary at Sony, particularly in direct-to-consumer (DTC) services, such as games and entertainment content delivery, and we are considering various applications. The personalization of services is now commonplace, and high-quality personalization is key to improving the user experience and connecting with more users [2].
However, in practical terms, it is expensive to introduce a new decision-making policy into a production system because it is time-consuming to incorporate a new policy into a service, and the performance of that policy may be poor.
What is Off-Policy Evaluation?
Given the above-mentioned background, off-policy evaluation (OPE), a technique that applies causal inference, has become important because it enables us to evaluate the performance of a decision-making policy using logged data (i.e., offline evaluation). The formulation is as follows: We denote the user feature (context) by \(x\in\mathcal{X}\), the action on the user by \(a\in\mathcal{A}\), and the observed reward by \(r\in[0,r_{\rm{max}}]\). Hence, the logged data is \(\mathcal{D}_{b}:=\{(x_i,a_i,r_i)\}_{i=1}^{n}\). The decision-making policy used to collect the logged data is called the behavior policy and denoted by \(\pi_b\) (Figure 1).
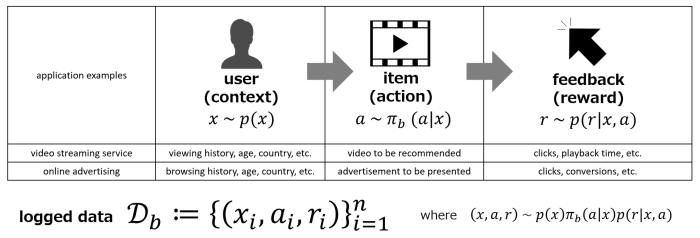
We want to know the performance of a new policy \(\pi_e\) (evaluation policy), which is different from the behavior policy \(\pi_b\), and its performance is defined as the expected reward \(V(\pi_{e})\) when it is deployed online (Figure 2). The goal of OPE is to estimate the performance of evaluation policy \(\pi_e\) accurately using the logged data \(\mathcal{D}_b\) offline.
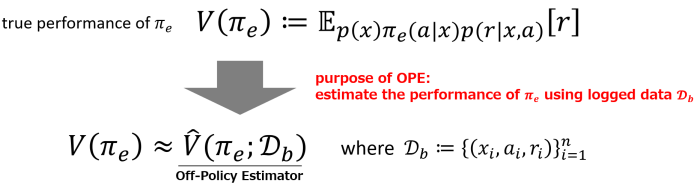
Many estimation methods (off-policy estimators \(\hat{V}(\pi_{e};\mathcal{D}_b)\)) have been proposed. Typical estimators are inverse propensity scoring (IPS, or inverse probability weighting (IPW) in some papers) [3,4], direct method (DM) [5], and doubly robust (DR) estimators [6]:
\(\hat{V}_{\rm{IPS}}(\pi_{e};\mathcal{D}_{b}):=\frac{1}{n}\sum_{i=1}^{n}w(x_i,a_i)r_i\) where \(w(x,a):=\frac{\pi_e(a|x)}{\pi_b(a|x)}\) (importance weight),
\(\hat{V}_{\rm{DM}}(\pi_{e};\mathcal{D}_{b},\hat{q}):=\frac{1}{n}\sum_{i=1}^{n}\sum_{a\in\mathcal{A}}\pi_{e}(a|x_i)\hat{q}(x_i,a)\) where \(\hat{q}(x,a)\approx q(x,a):=\mathbb{E}[r|x,a]\),
\(\hat{V}_{\rm{DR}}(\pi_{e};\mathcal{D}_{b},\hat{q}):=\frac{1}{n}\sum_{i=1}^{n}w(x_i,a_i)(r_i -\hat{q}(x_i,a_i))+\hat{V}_{\rm{DM}}(\pi_{e};\mathcal{D}_{b},\hat{q})\).
Each off-policy estimator has unique characteristics. For example, IPS is an unbiased estimator and its variance tends to be large when the importance weight is large, whereas DM is not an unbiased estimator and its variance tends to be smaller than that of IPS. Many other advanced off-policy estimators have been proposed; hence, if you are interested, that are available in the literature.
Challenge in Off-Policy Evaluation
As we have mentioned, OPE is a technique that can solve the important practical problems and is an area of active research. A number of off-policy estimators have been proposed, and at first glance, it would seem that OPE has become more practical and easier to use. However, a major challenge remains: the matter of which off-policy estimator to use. The best off-policy estimator depends on configurations, such as the number of actions, sample size, behavior policy \(\pi_b\), and evaluation policy \(\pi_e\). It is empirically known that no single estimator dominates the others [7]. Therefore, to conduct OPE, it is necessary to select an off-policy estimator that is appropriate for the evaluation policy \(\pi_e\) and the data to be processed. This process is called estimator selection.
Proposed Method
Our team has developed a method that enables practitioners to select an appropriate estimator adaptively for a given configuration, which we presented at AAAI2023 [1]. In the following, we provide a brief explanation of our proposed method.
First, we introduce the formulation of estimator selection (Figure 3). The performance of an off-policy estimator is defined as the mean squared error (MSE) of the true and estimated performance of the policy. Estimator selection aims to select an off-policy estimator that minimizes the MSE. However, the MSE cannot be calculated directly because the true performance of the policy is unknown. Therefore, we need to select an off-policy estimator based on an estimated mean squared error \(\hat{\rm{MSE}}\).
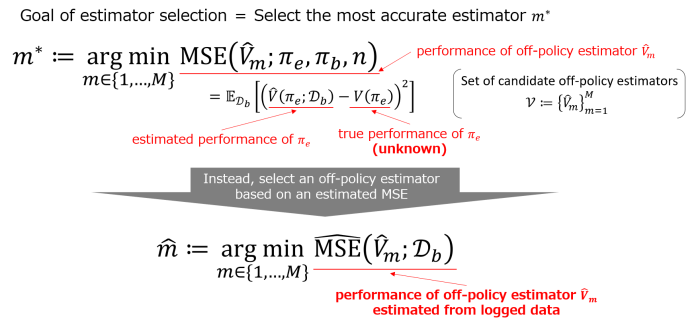
Figure 4 shows the non-adaptive heuristic, which is the estimator selection procedure used in the existing papers [8,9]. We assume that logged data \(\mathcal{D}_b\) is collected through the A/B testing of two policies \(\pi_A\) and \(\pi_B\). Then, we consider \(\pi_B\) as the pseudo behavior policy and \(\pi_A\) as the pseudo evaluation policy. Leveraging on-policy estimation instead of the unknown true policy performance, we can estimate the MSE. Then, we select the off-policy estimator with the lowest estimated MSE.
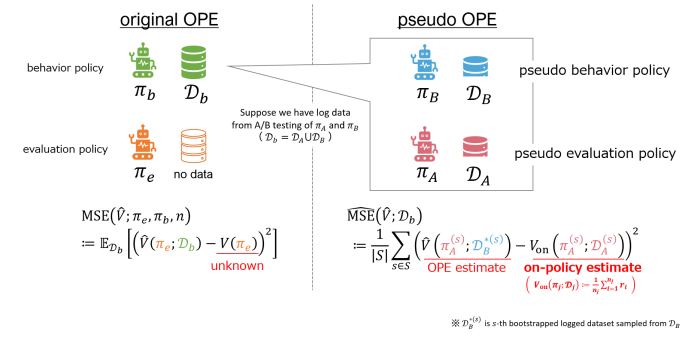
However, the non-adaptive heuristic has a critical pitfall. As we mentioned, the optimal off-policy estimator depends on the evaluation policy \(\pi_e\). However, the non-adaptive heuristic is not adaptive to \(\pi_e\) and selects the same off-policy estimator for any \(\pi_e\). This means that it may select an inappropriate off-policy estimator for a given evaluation policy. For example, if \(\pi_e\) and \(\pi_A\) deviate greatly, it is easy to see that it becomes difficult to estimate the MSE accurately. This would result in the inaccurate estimation of the performance of \(\pi_e\).
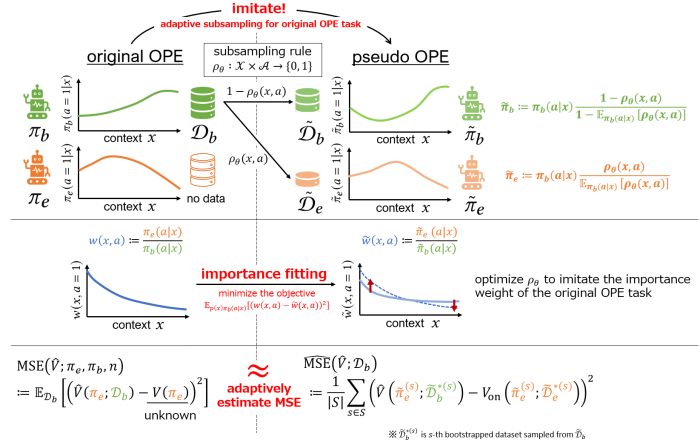
Our team proposed a method called policy-adaptive estimator selection via importance fitting (PAS-IF) [1] to select an appropriate off-policy estimator for a given evaluation policy \(\pi_e\). The basic idea is shown in Figure 5. We want to estimate the MSE in the original OPE task. Hence, we consider splitting the logged data \(\mathcal{D}_b\) to imitate the behavior policy \(\pi_b\) and evaluation policy \(\pi_e\) as much as possible. In PAS-IF, we take particular note of importance weight \(w(x,a):=\frac{\pi_e(a|x)}{\pi_b(a|x)}\), which characterizes the relationship between behavior policy \(\pi_b\) and evaluation policy \(\pi_e\). By optimizing the way data are subsampled to imitate the importance weight of the original OPE task, we can adaptively construct data as if it were collected by the pseudo behavior policy and pseudo evaluation policy. The subsequent procedure is the same as that in the non-adaptive heuristic. We estimate the MSE using on-policy estimation instead of the unknown true policy performance, and select the off-policy estimator with the lowest estimated MSE. This adaptive subsampling of data and MSE estimation allow us to select the most appropriate off-policy estimator from a number of candidates for a given \(\pi_e\). If you are interested in specific algorithms and experimental results, please refer to the paper [1]. As a future work, we would like to consider applying our proposed method to OPE in reinforcement learning, which is a more complex problem.
About Recruitment
At Sony, we will continue to conduct academic and practical research on the personalization of decision-making and improvement of actions, including OPE explained in this article. If you are interested in this area, please visit this page. Additionally, by selecting the Technology Category “Machine Learning,” or “Data Analysis,” you can find related job openings.
References
[1] Udagawa, T.; Kiyohara, H.; Narita, Y.; Saito, Y.; and Tateno, K. 2023. Policy-Adaptive Estimator Selection for Off-Policy Evaluation. Proceedings of the AAAI Conference on Artificial Intelligence, 37(8), 10025-10033. https://doi.org/10.1609/aaai.v37i8.26195
[2] https://wpengine.com/gen-z-eu/
[3] Precup, D.; Sutton, R. S.; and Singh, S. P. 2000. Eligibility Traces for Off-Policy Policy Evaluation. In Proceedings of the 17th International Conference on Machine Learning, 759–766. https://dl.acm.org/doi/10.5555/645529.658134
[4] Strehl, A.; Langford, J.; Li, L.; and Kakade, S. M. 2010. Learning from Logged Implicit Exploration Data. In Advances in Neural Information Processing Systems, volume 23, 2217–2225. https://arxiv.org/abs/1003.0120
[5] Beygelzimer, A.; and Langford, J. 2009. The Offset Tree for Learning with Partial Labels. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 129–138. https://dl.acm.org/doi/10.1145/1557019.1557040
[6] Dudík, M.; Erhan, D.; Langford, J.; and Li, L. 2014. Doubly Robust Policy Evaluation and Optimization. Statistical Science, 29(4): 485–511. https://arxiv.org/abs/1503.02834
[7] Saito, Y.; Joachims, T. 2022. Counterfactual Evaluation and Learning for Interactive Systems. KDD Tutorial, https://counterfactual-ml.github.io/kdd2022-tutorial/
[8] Saito, Y.; Aihara, S.; Matsutani, M.; and Narita, Y. 2021a. Open Bandit Dataset and Pipeline: Towards Realistic and Reproducible Off-Policy Evaluation. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track. https://arxiv.org/abs/2008.07146
[9] Saito, Y.; Udagawa, T.; Kiyohara, H.; Mogi, K.; Narita, Y.; and Tateno, K. 2021b. Evaluating the Robustness of Off-Policy Evaluation. In Proceedings of the 15th ACM Conference on Recommender Systems, 114–123. https://dl.acm.org/doi/10.1145/3460231.3474245