因果推論による個人化アルゴリズムのオフライン評価

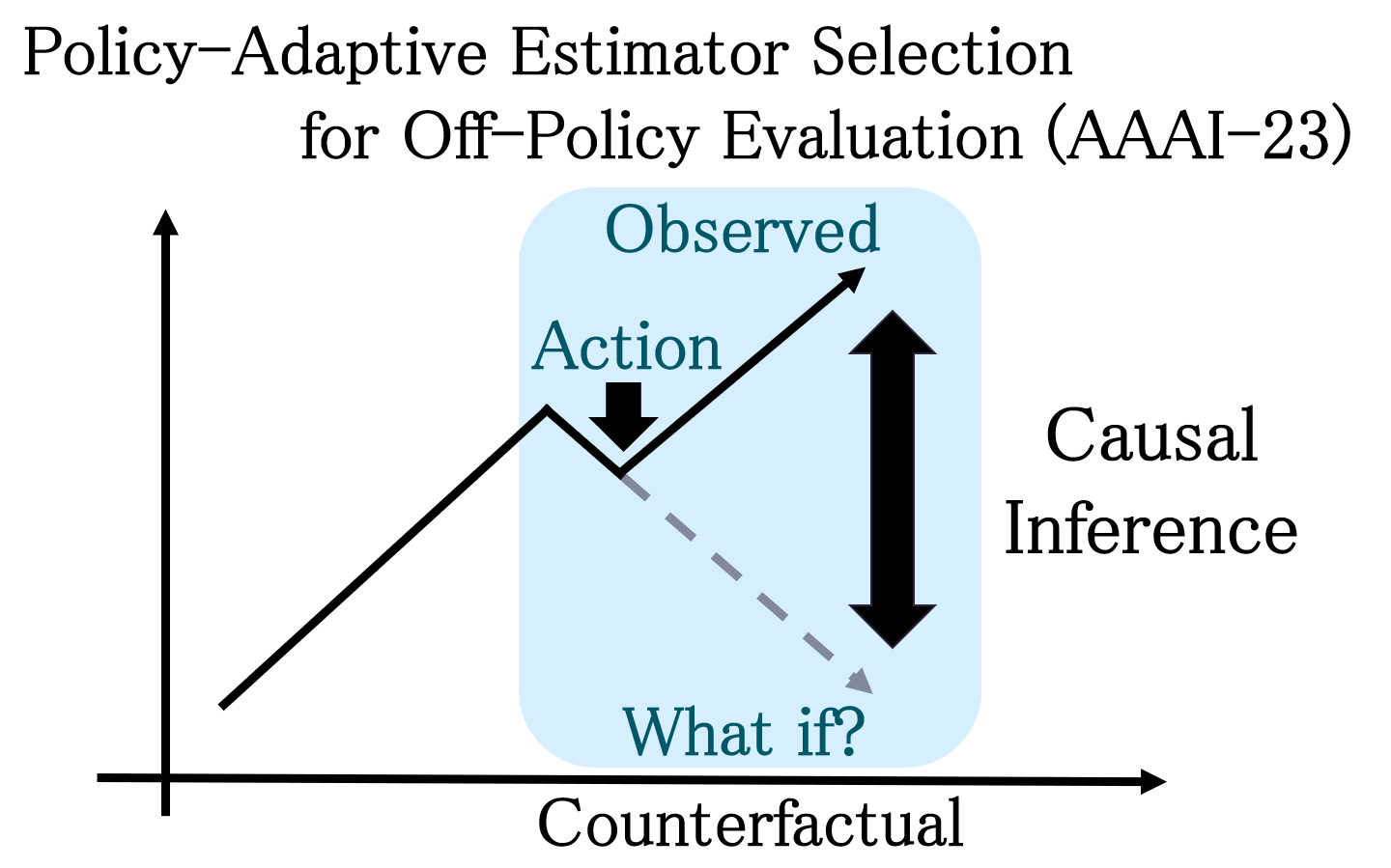
はじめに

ソニーグループ株式会社で機械学習・因果推論の研究開発をしている宇田川拓麻です。この記事では、意思決定アルゴリズムのオフライン評価に関する基礎的事項と、我々がAAAI2023で発表した論文[1]について紹介したいと思います。

背景

動画配信サービスにおける推薦、ネット広告の表示、メルマガの個人化など、昨今あらゆる場面でサービス側からユーザに対して何かしらのactionをする意思決定がなされています。とりわけ、過去に収集されたログデータを学習した機械学習モデルによる意思決定方策（policy）は、Key Performance Indicator（KPI）の改善において重要な役割を果たしています。

意思決定方策の最適化は、ソニーにおいても特にゲームやエンタテインメントコンテンツの配信といったDTC（Direct-to-Consumer）サービスで必要となり、様々なアプリケーションが検討されています。サービスの個人化はもはや当たり前のこととなっており、質の高い個人化はユーザ体験を向上させ、より多くのユーザとつながる鍵となります[2]。

しかし、そのような意思決定方策をいきなり本番システムに導入するのは実務上コストが高いです。なぜなら、新しい意思決定方策をサービスに組み込むには手間がかかる上に、その意思決定方策の性能が悪い可能性があるからです。

Off-Policy Evaluationとは

そこで重要になってくるのが、因果推論の手法を応用したOff-Policy Evaluation（OPE、オフ方策評価）という技術です。OPEは、ログデータを使った（＝オフラインでの）意思決定方策の性能評価を可能にします。具体的な定式化は次のようになります。ユーザ特徴量（context）を\(x\in\mathcal{X}\)、ユーザに対するactionを\(a\in\mathcal{A}\)、観測される報酬を\(r\in[0,r_{\rm{max}}]\)とします。したがって、ログデータは\(\mathcal{D}_{b}:=\{(x_i,a_i,r_i)\}_{i=1}^{n}\)となります。また、ログデータ収集時に使用していた意思決定方策を行動方策（behavior policy）と呼び、ここでは\(\pi_b\)と書くことにします（図1）。

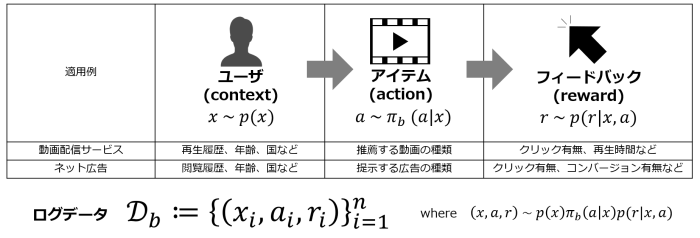
さて、我々は行動方策\(\pi_b\)とは別の新しい意思決定方策\(\pi_e\)（evaluation policy、評価方策）の性能を知りたいわけですが、その性能は方策をオンラインに導入した際の期待報酬\(V(\pi_{e})\)として定義されます（図2）。OPEのゴールは、\(\pi_e\)の性能をログデータ\(\mathcal{D}_b\)を使ってオフラインで正確に推定することです。

推定方法（オフ方策推定量、\(\hat{V}(\pi_{e};\mathcal{D}_b)\)）は多くの種類が提案されていますが、標準的なものとしてはInverse Propensity Scoring（IPS、文献によってはInverse Probability Weighting（IPW）と記載）[3,4]、Direct Method（DM）[5]、Doubly Robust（DR） [6]といったものがあります。

\(\hat{V}_{\rm{IPS}}(\pi_{e};\mathcal{D}_{b}):=\frac{1}{n}\sum_{i=1}^{n}w(x_i,a_i)r_i\)  where \(w(x,a):=\frac{\pi_e(a|x)}{\pi_b(a|x)}\) (importance weight),

\(\hat{V}_{\rm{DM}}(\pi_{e};\mathcal{D}_{b},\hat{q}):=\frac{1}{n}\sum_{i=1}^{n}\sum_{a\in\mathcal{A}}\pi_{e}(a|x_i)\hat{q}(x_i,a)\)  where \(\hat{q}(x,a)\approx q(x,a):=\mathbb{E}[r|x,a]\),

\(\hat{V}_{\rm{DR}}(\pi_{e};\mathcal{D}_{b},\hat{q}):=\frac{1}{n}\sum_{i=1}^{n}w(x_i,a_i)(r_i -\hat{q}(x_i,a_i))+\hat{V}_{\rm{DM}}(\pi_{e};\mathcal{D}_{b},\hat{q})\).

IPSは不偏推定量ですがimportance weightが大きくなるような状況だと分散が大きくなり、逆にDMは不偏推定量ではないですがIPSと比べて分散が小さくなる傾向にあるなど、各オフ方策推定量にはそれぞれ特徴があります。他にも発展的なオフ方策推定量は数多く提案されているので、興味がある方は調べてみてもよいでしょう。

Off-Policy Evaluationにおける課題

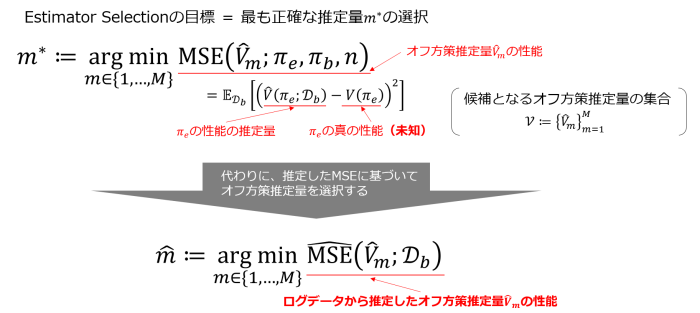
ここまで説明してきたように、OPEは実務的に重要な課題を解決しうる技術であり、活発に研究されている分野です。数多くのオフ方策推定量も提案され、一見すると実務でOPEを活用しやすくなったように思われます。しかし、大きな課題が残っています。それは、どのオフ方策推定量を使えばいいのか、という問題です。Action数、サンプルサイズ、行動方策\(\pi_b\)、評価したい方策\(\pi_e\)などといったconfigurationによってベストなオフ方策推定量は変わり、常に正確なオフ方策推定量はないことが実験的に知られています[7]。したがって、OPEを実践するためには、自分が扱っているデータや評価したい方策\(\pi_e\)に適したオフ方策推定量を選択する必要があり、これをEstimator Selectionと呼びます。

解決手法の提案

我々のチームでは、与えられた状況において最適なオフ方策推定量を適応的に選択する手法を開発し、AAAI2023にて発表しました[1]。以下では、その内容を簡単に紹介します。

まず、Estimator Selectionの定式化を紹介します（図3）。オフ方策推定量の性能は方策の真の性能と推定性能のMean Squared Error（MSE）として定義され、Estimator SelectionではMSEを最小にするようなオフ方策推定量の選択を目指します。しかし、方策の真の性能は未知のためMSEを直接計算することはできません。したがって、何らかの方法で推定した\(\hat{\rm{MSE}}\)に基づいてオフ方策推定量を選択していくことになります。

既存の論文で使われていた手順（Non-Adaptive Heuristic）[8,9]を図4で簡単に説明しています。ログデータ\(\mathcal{D}_b\)は2つの方策\(\pi_A\),\(\pi_B\)のA/Bテストによって集められていたと仮定します。この時、片方を疑似的な行動方策\(\pi_B\)、もう片方を疑似的な評価方策\(\pi_A\)と捉えます。本来は未知である真の方策性能については、on-policyで算出した性能を使うことで、MSEを推定できます。そして、推定されたMSEが最小のオフ方策推定量を選択することになります。

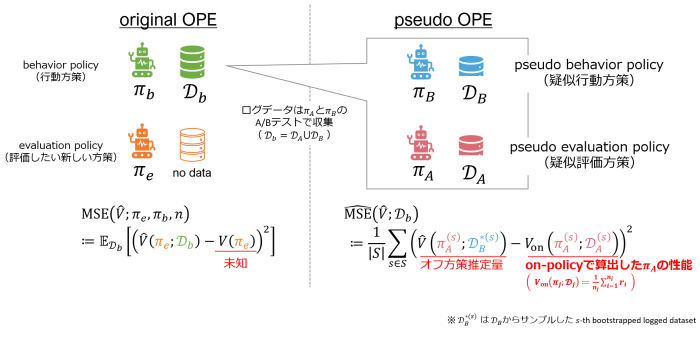
ただ、このNon-Adaptive Heuristicには大きな欠点があります。先に述べたように、最適なオフ方策推定量は評価方策\(\pi_e\)によって変わります。しかし、Non-Adaptive Heuristicは\(\pi_e\)に対して適応的ではなく、どのような\(\pi_e\)に対しても単一のオフ方策推定量を選択します。したがって、評価方策\(\pi_e\)によっては不適切なオフ方策推定量を選択してしまいます。例えば、\(\pi_e\)と\(\pi_A\)が大きく乖離しているとMSEの正確な推定が難しそうであることは容易に想像がつくと思います。そうすると、結果として\(\pi_e\)の性能を誤って見積もってしまうことになります。

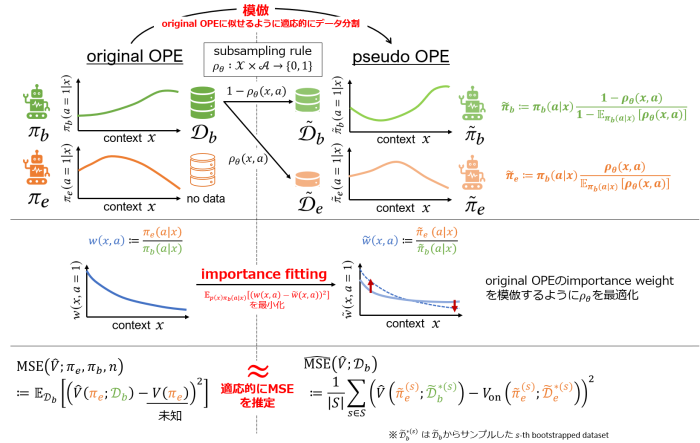
そこで我々のチームでは、与えられた評価方策\(\pi_e\)に対して適切なオフ方策推定量を選択するPolicy-Adaptive Estimator Selection via Importance Fitting（PAS-IF）という手法を提案しました[1]。基本的なアイディアを図5に示しています。我々が推定したいのは元々のOPEタスクにおけるMSEです。そこで、行動方策\(\pi_b\)や評価方策\(\pi_e\)をできるだけ模倣するようにログデータ\(\mathcal{D}_b\)を分割することを考えます。特にPAS-IFでは、行動方策\(\pi_b\)と評価方策\(\pi_e\)の関係を特徴づけるimportance weight \(w(x,a):=\frac{\pi_e(a|x)}{\pi_b(a|x)}\)に注目しています。すなわち、元々のOPEにおけるimportance weightを模倣するようにデータの分割の仕方を最適化することで、疑似的な行動方策・評価方策で収集されたようなデータを適応的に構築することができます。その後の手順はNon-Adaptive Heuristicと同じで、本来は未知である真の方策性能についてはon-policyで算出した性能を使ってMSEを推定し、推定されたMSEが最小のオフ方策推定量を選択することになります。このように適応的なデータの分割およびMSEの推定をすることで、与えられた\(\pi_e\)に応じて数多くのオフ方策推定量の中から最も適切なものを選択できるようになります。より具体的なアルゴリズムや実験結果について気になる方は論文[1]を参照していただければと思います。今後は、より複雑な問題である強化学習でのOPEに応用することも検討していきたいと考えています。

最後に

ここで紹介したOPEも含めて、ソニーでは今後も意思決定の個人化や施策の改善について（アカデミックなものも実務的なものも）研究開発していきます。採用に関してはこちらのページで「因果推論」「個人化」「機械学習」などで検索していただくと関連する求人中のポジションがヒットするので、ご興味のある方は見ていただければと思います。

References

[1] Udagawa, T.; Kiyohara, H.; Narita, Y.; Saito, Y.; and Tateno, K. 2023. Policy-Adaptive Estimator Selection for Off-Policy Evaluation. Proceedings of the AAAI Conference on Artificial Intelligence, 37(8), 10025-10033. https://doi.org/10.1609/aaai.v37i8.26195

[2] https://wpengine.com/gen-z-eu/

[3] Precup, D.; Sutton, R. S.; and Singh, S. P. 2000. Eligibility Traces for Off-Policy Policy Evaluation. In Proceedings of the 17^th International Conference on Machine Learning, 759–766. https://dl.acm.org/doi/10.5555/645529.658134

[4] Strehl, A.; Langford, J.; Li, L.; and Kakade, S. M. 2010. Learning from Logged Implicit Exploration Data. In Advances in Neural Information Processing Systems, volume 23, 2217–2225. https://arxiv.org/abs/1003.0120

[5] Beygelzimer, A.; and Langford, J. 2009. The Offset Tree for Learning with Partial Labels. In Proceedings of the 15^th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 129–138. https://dl.acm.org/doi/10.1145/1557019.1557040

[6] Dudík, M.; Erhan, D.; Langford, J.; and Li, L. 2014. Doubly Robust Policy Evaluation and Optimization. Statistical Science, 29(4): 485–511. https://arxiv.org/abs/1503.02834

[7] Saito, Y.; Joachims, T. 2022. Counterfactual Evaluation and Learning for Interactive Systems. KDD Tutorial, https://counterfactual-ml.github.io/kdd2022-tutorial/

[8] Saito, Y.; Aihara, S.; Matsutani, M.; and Narita, Y. 2021a. Open Bandit Dataset and Pipeline: Towards Realistic and Reproducible Off-Policy Evaluation. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track. https://arxiv.org/abs/2008.07146

[9] Saito, Y.; Udagawa, T.; Kiyohara, H.; Mogi, K.; Narita, Y.; and Tateno, K. 2021b. Evaluating the Robustness of Off-Policy Evaluation. In Proceedings of the 15th ACM Conference on Recommender Systems, 114–123. https://dl.acm.org/doi/10.1145/3460231.3474245